When we look at a seemingly simple value like “8.58461538/100,” it may not immediately convey a lot of information. However, this number can play an important role in various areas, particularly in statistical analysis, research, and data interpretation.
In this comprehensive article, we will delve deeply into the meaning, usage, and implications of “8.58461538/100” in statistical contexts, and explore related concepts that help illuminate its significance. We’ll provide clear explanations, real-world examples, and practical applications for readers who may be new to statistical analysis.
What is “8.58461538/100”?
The term “8.58461538/100” can be interpreted as a percentage or a fraction. When we divide 8.58461538 by 100, we get 0.0858461538, which is equivalent to approximately 8.58%. This value is often encountered in statistical contexts where percentages are used to express probabilities, proportions, and other metrics that compare values relative to a total.
Simplifying the Value of “8.58461538/100”!
To better understand “8.58461538/100,” let’s break it down:
- Conversion to Decimal: When we divide 8.58461538 by 100, the result is 0.0858461538.
- Expressed as a Percentage: This can be rounded to approximately 8.58%, which makes it easier to use in discussions about statistical analysis or data interpretation.
In real-world terms, expressing a value as a percentage provides a clear understanding of its relative magnitude. For example, if you achieve an 8.58% increase in sales, it indicates that the sales performance improved by 8.58% relative to the baseline.
The Role of Percentages in Statistics!
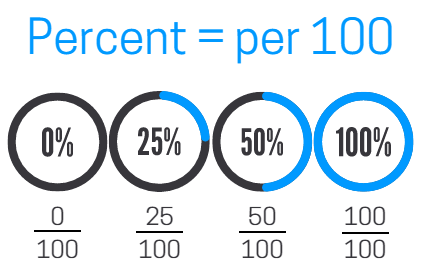
Percentages are widely used in statistics to represent data in a way that is easy to understand. They help us compare proportions, evaluate probabilities, and assess the relative significance of different values. Here are some common applications:
- Survey Results: Percentages express how many respondents selected a particular choice.
- Risk Assessment: Percentages are used to communicate probabilities or risks.
- Statistical Significance Testing: Percentages can determine the likelihood of an event occurring by chance.
Interpreting “8.58461538/100” in Statistical Analysis
When we look at “8.58461538/100,” the value can be used to represent various statistical metrics, including:
- Error Rates: In hypothesis testing, a percentage such as 8.58% may represent an acceptable error rate for making decisions based on data.
- Confidence Intervals: A percentage can also be used to describe the range of values within which we expect a certain parameter to fall.
- Probabilities: Percentages frequently express the chance of an event occurring within a given dataset.
Understanding how to interpret and use percentages correctly can help avoid errors in analysis, leading to more accurate conclusions.
Understanding Type I and Type II Errors!
To appreciate the significance of “8.58461538/100,” we need to understand some common errors in statistical testing:
- Type I Error (False Positive): This occurs when we reject a true null hypothesis, essentially finding a significant effect when there is none.
- Type II Error (False Negative): This happens when we fail to reject a false null hypothesis, meaning we miss detecting an effect that actually exists.
Balancing the risks of these errors is crucial for accurate statistical analysis. A threshold like “8.58461538/100” (or 8.58%) might be used as a cut-off to determine when to accept or reject a hypothesis, helping to manage the likelihood of errors.
How “8.58461538/100” Affects Statistical Power?

Statistical power refers to the ability of a test to detect an effect if there is one. The value “8.58461538/100” could be related to the power of a test in several ways:
- Setting Power Thresholds: Power is often expressed as a percentage, and researchers might aim for a power of 80% or higher.
- Significance Levels: An 8.58% significance level would be relatively high, indicating a lenient threshold for rejecting the null hypothesis. Lower significance levels (e.g., 5% or 1%) are more common in practice.
Using a value like 8.58% in statistical analysis could indicate a higher tolerance for Type I errors, possibly due to the nature of the research or the consequences of missing an effect.
Examples of Using “8.58461538/100” in Research!
To illustrate the practical use of “8.58461538/100,” consider the following scenarios:
- Medical Studies: Suppose researchers are testing the effectiveness of a new treatment. They may use an 8.58% threshold for statistical significance if the consequences of Type II errors (missing a beneficial treatment) outweigh the risk of Type I errors.
- Marketing Campaign Analysis: If a company wants to determine whether a new advertisement significantly increases customer engagement, they might use 8.58% as a significance level to assess the campaign’s effectiveness.
These examples show how context determines the choice of statistical thresholds.
The Connection Between “8.58461538/100” and Significance Testing!
Significance testing involves comparing observed data with a predetermined threshold to assess whether an effect is statistically meaningful.
- Using 8.58% as a Threshold: While more conventional significance levels are 5% (0.05) or 1% (0.01), using a threshold like 8.58% may be appropriate for exploratory studies where higher error risks are acceptable.
- Interpreting P-Values: If a p-value is below the chosen significance level, we reject the null hypothesis. For example, if we set a threshold at 8.58%, any p-value below 0.0858 would lead to rejecting the null hypothesis.
Practical Applications in Real-World Scenarios!
The concept of “8.58461538/100” can be applied in numerous fields, such as:
- Economics: Evaluating economic indicators that show growth rates or changes in key metrics.
- Environmental Studies: Assessing the probability of certain outcomes in ecological research.
- Quality Control in Manufacturing: Using percentages to measure defect rates or compliance with standards.
In each case, interpreting the percentage correctly ensures accurate decision-making.
Common Mistakes When Interpreting Statistical Values!
Here are some common errors people make when working with percentages in statistics:
- Misunderstanding the Scale: Failing to recognize the difference between small changes in percentages and their real-world impact.
- Ignoring Context: Not considering the research context when choosing a significance level, which could lead to misinterpretation of results.
- Confusing Probability with Certainty: Percentages represent likelihoods, not guarantees, so results should be interpreted cautiously.
Related Concepts and Terms Explained!
- P-Value: A measure of the probability that observed results occurred by chance.
- Confidence Interval: A range of values that likely contains the true population parameter.
- Alpha Level: The threshold used to determine statistical significance, often set at 0.05 (5%) but potentially higher or lower depending on the context.
- Statistical Significance: Indicates whether the results of an analysis are unlikely to have occurred by random chance.
Frequently Asked Questions (FAQs):
What does “8.58461538/100” mean in statistics?
It means 8.58%, which can be used to represent probabilities, error rates, or significance levels in statistical analysis.
Why would someone use an 8.58% significance level?
In exploratory studies or situations where the cost of missing an effect is high, a higher significance level like 8.58% may be more appropriate.
Is “8.58461538/100” commonly used in statistical testing?
While more conventional thresholds are 5% or 1%, using 8.58% could be suitable in specific contexts or preliminary research.
How does “8.58%” compare to other significance levels?
It is more lenient than the common 5% level, meaning there is a higher chance of rejecting the null hypothesis when it is true.
Conclusion:
In summary, the value “8.58461538/100” is more than just a number. It embodies concepts fundamental to statistical analysis, such as significance testing, error rates, and statistical power. Understanding its implications allows researchers, analysts, and decision-makers to make informed choices based on data, ultimately leading to better outcomes across various fields.
